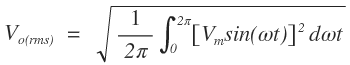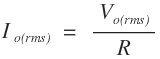Single Phase Half Wave Uncontrolled Rectifier with R Load

In this article, we will see the analysis of Single Phase Half Wave Uncontrolled Rectifier with Resistive (R) Load as shown in Figure 1. V_s is supply and ‘i_s‘ is the source current. V_D and ‘i_D‘ is the diode voltage and current respectively. V_o and ‘i_o‘ is the load voltage and current respectively.

V_s = V_msin(ωt)

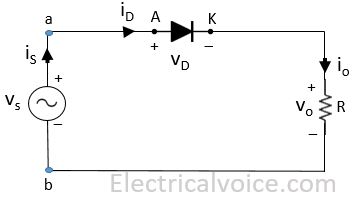
Step-1: Write KVL in the given circuit

v_s − v_D − v_o = 0

v_ab = v_s = v_D + v_o

v_ab = v_s = V_msin(ωt)

v_ba = − v_ab = − V_msin(ωt)

Step-2: Device working status

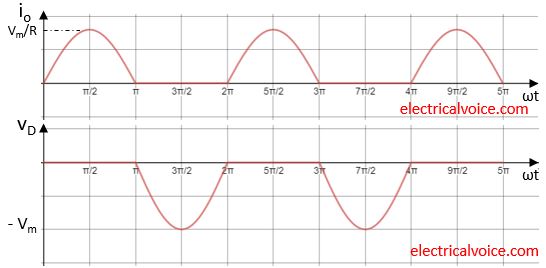
In the positive half cycle, the diode is forward biased and is turned ON at ωt = 0°.

At ωt = π, the current through the diode falls to zero i.e. below zero and simultaneously a reverse voltage appears across the diode and it turns OFF.

1). 0 < ωt < π

Diode is forward biased. Hence turns ON

v_D = 0 V

v_o = v_ab = V_msin(ωt)

i_o = i_s = i_D = (v_o)/R = (V_msin(ωt))/R

2). π < ωt < 2π

Diode is reversed biased. Hence turns OFF

i_o = i_s = i_D = 0 A

v_o = 0 V

v_D = v_ab = V_msin(ωt)

3). 2π < ωt < 3π

Diode is forward biased. Hence turns ON

v_D = 0 V

v_o = v_ab = V_msin(ωt)

i_o = i_s = i_D = (v_o)/R = (V_msin(ωt))/R

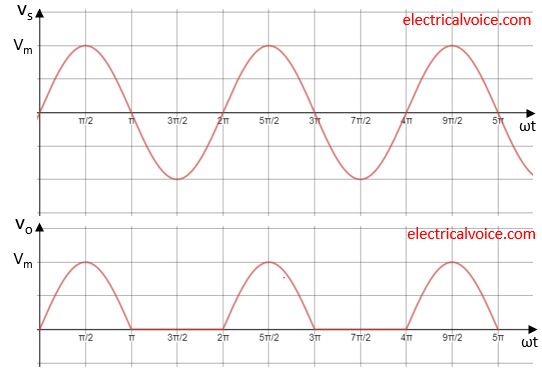
The waveforms for load voltage(v_o), and current(i_o), diode voltage(v_D) is shown in figure 2. The waveforms of supply current and diode current is same as load current.

Note: For a resistive load, v_o and i_o waveform will be same in nature except in magnitude.

Step-3:

1). Diode starts conducting at  ωt = 0°

2). Extinction angle (β) = π

3). Conduction angle (γ) = β − 0 = π − 0 = π

4). Conduction time (t_c) = γ/ω = π /ω

5). Diode reverse biased time = (2π − π)/ω = π/ω

6). Peak Inverse voltage (PIV) = V_m

Step-4:

Average Values

The average output voltage V_o(avg) across load R is given by

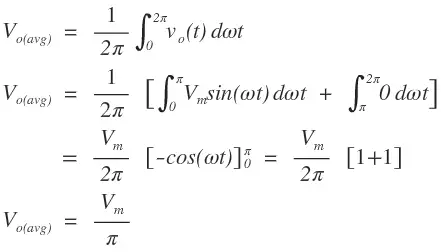
The average output current I_o(avg) through the load R is given by

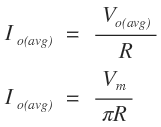
RMS values