Log amplifier or logarithmic amplifier is an electronic circuit that produces output that is proportional to the logarithm of the applied input. Basically it performs mathematical operation of a logarithm. In this article, we will see the different log amplifier circuits, its working and log amplifier applications. Basically two circuits are there to perform the logarithmic function. First, using diode and op-amp and second, using BJT and op-amp.
Log amplifier using diode and op-amp
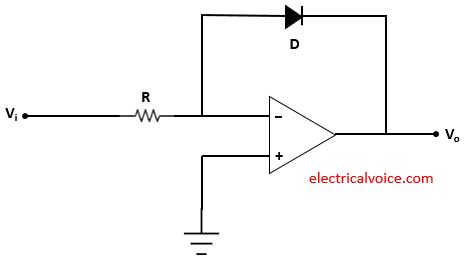
Diode, resistor and op-amp used in the log amplifier as shown in figure 1. The input Vi is applied through resistor R at the inverting terminal. Vo is the output voltage. The non-inverting terminal of the op-amp is connected to the ground. This means that the voltage of the non-inverting terminal is zero volts.
Analysis
The analysis of the log amplifier is shown in figure 2. Since the op-amp is ideal and negative feedback is present, the voltage of the inverting terminal (V−) is equal to the voltage of the non-inverting terminal (V+ = 0V), according to the virtual short concept.
V− = V+ = 0V
The currents entering both terminals of the op-amp are zero since the op-amp is ideal.
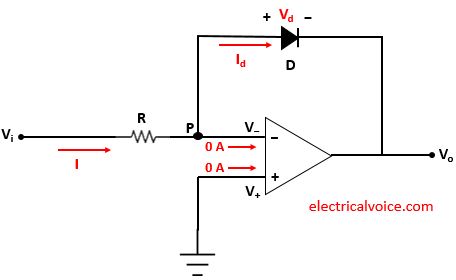
Let current I flows through the resistor R.
\begin{equation} \label{eq:poly}
I=\frac{V_{i}-0}{R}=\frac{V_{i}}{R}
\end{equation}
and diode current $I_{d}$,
\begin{equation} \label{eq:poly}
I_{d}=I_{o}e^{\frac{V_{d}}{\eta V_{T}}}
\end{equation}
where $V_d$ = forward bias voltage across diode D
Apply KCL at node P
$I = 0 + I_{d}$
\begin{equation} \label{eq:poly}
I = I_{d}
\end{equation}
and
$V_{d} = 0-V_{o}$
\[V_{d} = -V_{o}\]
Therefore, equation (2) becomes
\begin{equation} \label{eq:poly}
I_{d}=I_{o}e^{-\frac{V_{o}}{\eta V_{T}}}
\end{equation}
From equation (1), (3) and (4), we have
\[\frac{V_{i}}{R}=I_{o}e^{-\frac{V_{o}}{\eta V_{T}}}\]
\[\ln \frac{V_{i}}{I_{0}R}=-{\frac{V_{o}}{\eta V_{T}}}\]
Therefore, we have
\[
\quicklatex{color=”#000000″ size=20}
\boxed{V_{o}=-\eta V_{T}\ln \frac{V_{i}}{I_{0}R}}
\]
Note: The above circuit is valid only for $V_{i}>0$.
Note: The negative sign in the output signifies that there is a 180° phase difference between output and the applied input.
Log amplifier using diode and transistor
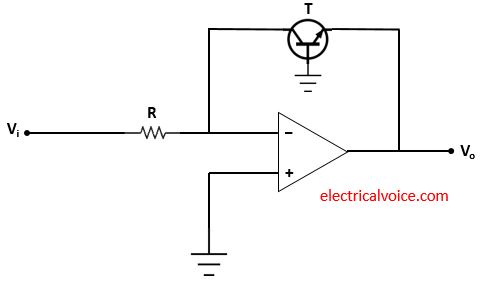
Another circuit comprises of a BJT (NPN) T, resistor (R) and op-amp used as the log amplifier as shown in figure 3. The input Vi is applied through resistor R at the inverting terminal. Vo is the output voltage. The non-inverting terminal of the op-amp is connected to the ground. This means that the voltage of the non-inverting terminal is zero volts.
Analysis
The analysis of the log amplifier is shown in figure 4. Since the op-amp is ideal and negative feedback is present, the voltage of the inverting terminal (V−) is equal to the voltage of the non-inverting terminal (V+ = 0V), according to the virtual short concept.
V− = V+ = 0V
The currents entering both terminals of the op-amp are zero since the op-amp is ideal.
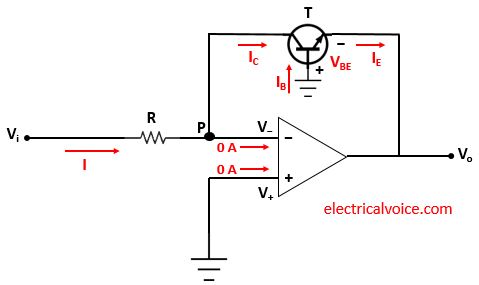
Let current I flows through the resistor R.
\begin{equation} \label{eq:poly}
I=\frac{V_{i}-0}{R}=\frac{V_{i}}{R}
\end{equation}
and collector current $I_{C}$,
\begin{equation} \label{eq:poly}
I_{C}=I_{s}e^{\frac{V_{BE}}{\eta V_{T}}}
\end{equation}
where $V_{BE} = V_B – V_E$
and Is = Reverse saturation current of emitter-base junction
As we know that
$I_C + I_B = I_E$
since IB ≅ 0 A
Therefore
\begin{equation} \label{eq:poly}
$I_C = I_E$
\end{equation}
Apply KCL at node P
$I = 0 + I_{C}$
\begin{equation} \label{eq:poly}
I = I_{C}
\end{equation}
and
$V_{BE} = 0-V_{o}$
\[V_{BE} = -V_{o}\]
Therefore, equation (6) becomes
\begin{equation} \label{eq:poly}
I_{C}=I_{s}e^{-\frac{V_{o}}{\eta V_{T}}}
\end{equation}
From equation (5), (7), (8) and (9), we have
\[\frac{V_{i}}{R}=I_{s}e^{-\frac{V_{o}}{\eta V_{T}}}\]
\[\ln \frac{V_{i}}{I_{s}R}=-{\frac{V_{o}}{\eta V_{T}}}\]
Therefore, we have
\[
\quicklatex{color=”#000000″ size=20}
\boxed{V_{o}=-\eta V_{T}\ln \frac{V_{i}}{I_{s}R}}
\]
Note: The negative sign in the output signifies that there is a 180° phase difference between output and the applied input.
Log amplifier Applications
1. It is used for measuring the signal strength.
