Op-amp Integrator is an electronic circuit that produces output that is proportional to the integration of the applied input. Basically it performs mathematical operation of integration. In this article, we will see the different op-amp based integrator circuits, its working and its applications. Basically two circuits are there to perform the integration function. First, using a capacitor and op-amp and second, using an inductor and op-amp.
Integrator circuit using capacitor and op-amp
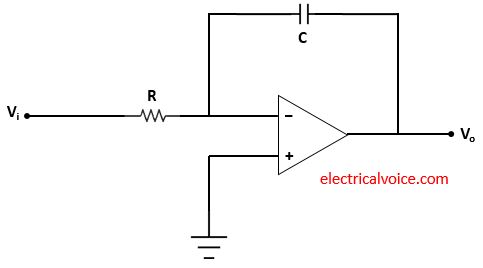
Capacitor (C), resistor (R) and op-amp are used in the integrator circuit as shown in figure 1. The input Vi is applied through resistor R at the inverting terminal. Vo is the output voltage. The non-inverting terminal of the op-amp is connected to the ground. This means that the voltage of the non-inverting terminal is zero volts.
Analysis
The analysis of the integrator circuit is shown in figure 2. Since the op-amp is ideal and negative feedback is present, the voltage of the inverting terminal (V−) is equal to the voltage of the non-inverting terminal (V+ = 0V), according to the virtual short concept.
V− = V+ = 0V
The currents entering both terminals of the op-amp are zero since the op-amp is ideal.
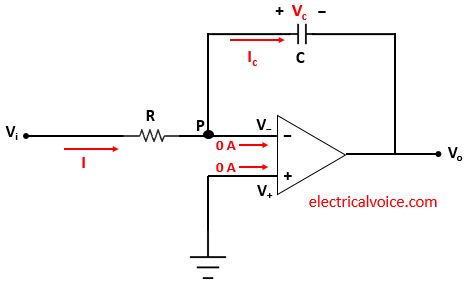
Let current I flows through the resistor R.
\begin{equation} \label{eq:poly}
I=\frac{V_{i}-0}{R}=\frac{V_{i}}{R}
\end{equation}
The voltage across capacitor (Vc) is given as
$V_c = 0-V_o$
\begin{equation} \label{eq:poly}
V_c=-V_{o}
\end{equation}
The capacitor current (Ic) is given as
\[I_{c}=C\frac{\mathrm{d} V_{c}}{\mathrm{d} t}\]
From equation (2), we have
\[I_{c}=C\frac{\mathrm{d} (-V_{o})}{\mathrm{d} t}=-C\frac{\mathrm{d} (V_{o})}{\mathrm{d} t}\]
Therefore
\begin{equation} \label{eq:poly}
I_{c}=-C\frac{\mathrm{d} V_{o}}{\mathrm{d} t}
\end{equation}
Apply KCL at node P
$I = 0 + I_{c}$
\begin{equation} \label{eq:poly}
I = I_{c}
\end{equation}
From equations (1), (3) and (4), we have
\[\frac{V_{i}}{R}=-C\frac{\mathrm{d} V_{o}}{\mathrm{d} t}\]
\[\Rightarrow \frac{\mathrm{d} V_{o}}{\mathrm{d} t}=-\frac{V_{i}}{RC}\]
\[\Rightarrow dV_{o}=-\frac{V_{i}}{RC}\, dt\]
Integrating both sides
\[\Rightarrow \int dV_{o}=-\frac{1}{RC}\int V_{i}\, dt\]
Therefore, we have
\[
\quicklatex{color=”#000000″ size=20}
\boxed{V_{o}=-\frac{1}{RC}\int V_{i}\, dt+K}
\]
where K is a constant
Note: The negative sign in the output signifies that there is a 180° phase difference between output and the applied input.
Integrator circuit using inductor and op-amp
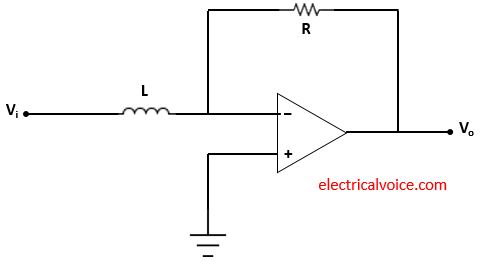
Inductor (L), resistor (R) and op-amp are used in the integrator circuit as shown in figure 3. The input Vi is applied through inductor L at the inverting terminal. Vo is the output voltage. The non-inverting terminal of the op-amp is connected to the ground. This means that the voltage of the non-inverting terminal is zero volts.
Analysis
The analysis of the integrator circuit is shown in figure 4. Since the op-amp is ideal and negative feedback is present, the voltage of the inverting terminal (V−) is equal to the voltage of the non-inverting terminal (V+ = 0V), according to the virtual short concept.
V− = V+ = 0V
The currents entering both terminals of the op-amp are zero since the op-amp is ideal.
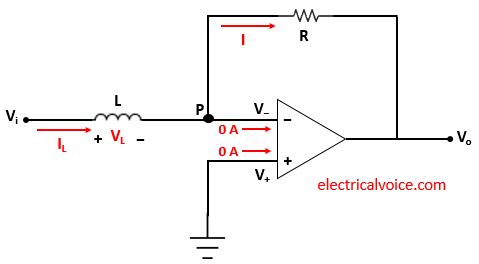
Let current I flows through the resistor R.
\begin{equation} \label{eq:poly}
I=\frac{0-V_{o}}{R}=-\frac{V_{o}}{R}
\end{equation}
Let IL is the inductor current
Apply KCL at node P
$I_L = 0 + I$
\begin{equation} \label{eq:poly}
I = I_{L}
\end{equation}
The voltage across inductor (VL) is given as
$V_L = V_i – 0$
\begin{equation} \label{eq:poly}
V_L=V_{i}
\end{equation}
The inductor voltage (VL) is given as
\[V_{L}=L\frac{\mathrm{d} I_{L}}{\mathrm{d} t}\]
From equations (5) and (6), we have
\[V_{L}=L\frac{\mathrm{d} (I_{L})}{\mathrm{d} t}=L\frac{\mathrm{d} (-\frac{V_o}{R})}{\mathrm{d} t}\]
Therefore
\begin{equation} \label{eq:poly}
\[V_{L}=-\frac{L}{R}\frac{\mathrm{d} V_o}{\mathrm{d} t}\]
\end{equation}
From equation (7), we have
\[V_{i}=-\frac{L}{R}\frac{\mathrm{d} V_o}{\mathrm{d} t}\]
\[\Rightarrow \frac{\mathrm{d} V_o}{\mathrm{d} t}= -\frac{R}{L}V_{i}\]
\[\Rightarrow dV_o= -\frac{R}{L}V_{i}\, dt\]
Integrating both sides
\[\Rightarrow \int dV_o= -\int \frac{R}{L}V_{i}\, dt\]
Therefore, we have
\[
\quicklatex{color=”#000000″ size=20}
\boxed{V_o= -\frac{R}{L}\int V_{i}\, dt+K}
\]
where K is a constant
Note: The negative sign in the output signifies that there is a 180° phase difference between output and the applied input.
