When two or more resistances are connected end to end consecutively, they are said to be connected in series. Figure 1 shows four resistances R1, R2, R3 and R4 which are connected in series. Resistances in series is denoted pictorially as shown in figure 2.
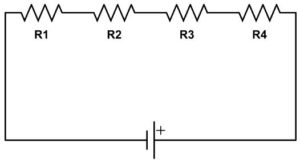

According to the law of combination of resistances in series, the combined resistance of any number of resistances connected in series is equal to the sum of the individual resistances.
For example, if a number of resistances R1, R2, R3, R4, ……….. , are connected in series, then the resultant resistance R is given by
R = R1+ R2+ R3+ R4+ ………..
Let 5 Resistances R1, R2, R3, R4, R5 are connected in series. R1= 5 Ω, R2= 3Ω, R3= 7Ω, R4= 4Ω, R5 = 10 Ω
Calculate combined resistance?
As we know that, if a number of resistances are connected in series, then the resultant resistance R is given by
R = R1+ R2+ R3+ R4+ R5
R = 5 + 3 + 7 + 4 + 10
R = 29 Ω
Following points should be remember
When a number of resistances are connected in series then
1. the sum of the potential differences across all the resistances is equal to the applied battery voltage.
2. the same current flows through each resistance (which is equal to the current flowing in the whole circuit).
