Causal Signal
A signal that does not start before t=0 is a causal signal i.e. x(t)=0, ∀ t<0.
Note: A system is causal or non-anticipatory if the output at any time to depends only on the values of the input at the present time and in the past. You can read about causal and non-causal systems in detail here.
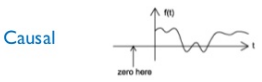
Note: All memoryless systems are causal systems since the output responds only to the current value of the input.
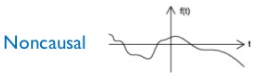
Non-Causal Signal
A signal that starts before t=0 is a non-causal signal.
Anti-Causal Signal
A signal that ends after t=0 is an anti-causal signal i.e. x(t)=0, ∀ t>0.

Note: Any signal x(t) that does not contain any singularities (a delta function or its derivative) at t=0 can be written as the sum of a causal part x+(t) and anti-causal part x−(t) i.e.
x(t) = x+(t) + x−(t)
For example, x(t) = e−at can be written as
x(t) = e−at u(t) + e−at u(−t)
causal anti-causal
Note: Multiplying the signal by the unit step ensure that the resulting signal is causal.
