In signal processing, signal undergoes several manipulations of independent variable i.e. time. Based upon that we can classify operation as
Operations corresponding to transformation of independent variable (Time)
- Time Shifting
- Time Scaling
- Time Reversal
Let us see each operation one by one.
Time Shifting
A signal x(t) may be shifted in time by replacing the independent variable t by either t−t0 or t+t0 . Here t0 is called as the shifting factor. Shifting in time may results in time delay or time advancement.
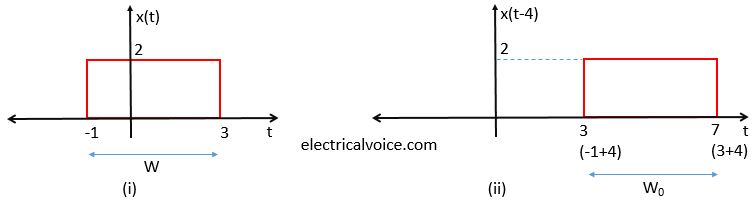
If the independent variable t is replaced by t−t0 ,the signal is shifted to the right and the time shift results in a delay of the signal by t0 units of time. This type of time shifting is known as Right side shifting. This can be achieved by adding t0 value to every time instant in signal x(t).
Consider a signal x(t) as shown in figure 1(i). Figure 1(ii) shows the signal x(t-4). During this process, the width of the signal x(t) does not change. Therefore W=W0.
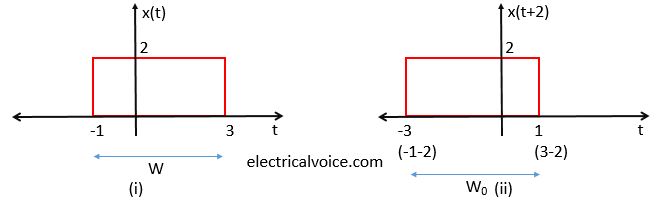
If the independent variable t is replaced by t+t0 ,the signal is shifted to the left and the time shift results in an advancement of the signal by t0 units of time. This type of time shifting is known as Left side shifting. This can be achieved by subtracting t0 value to every time instant in signal x(t).
Consider a signal x(t) as shown in figure 2(i). Figure 2(ii) shows the signal x(t+2). During this process, the width of the signal x(t) does not change. Therefore W=W0.
Time Scaling
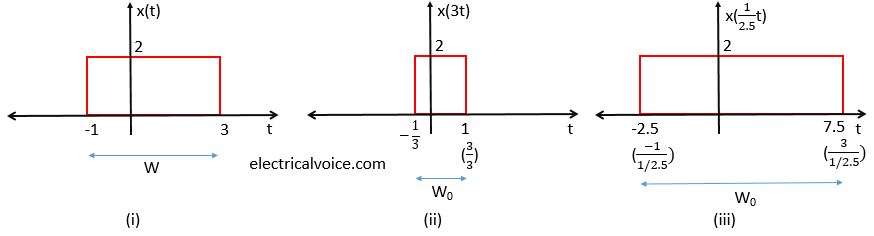
A signal x(t) may be scaled in time by replacing the independent variable t by at . Here ‘a’ is called as the scaling factor. Time scaling may results in signal compression or signal expansion.
If the independent variable t is replaced by at and a>1, the signal is compressed. This can be achieved by dividing every time instant in signal x(t) by ‘a‘.
If the independent variable t is replaced by at and 0<a<1, the signal is expanded. This can be achieved by dividing every time instant in signal x(t) by ‘a‘.
Consider a signal x(t) as shown in figure 3(i). Figure 3(ii) shows the signal x(3t). It is compressed since a>1. During this process, the width of the signal x(t) changes. Therefore W>W0. Figure 3(iii) shows the signal x((1/2.5)t). It is expanded since 0<a<1. During this process, the width of the signal x(t) changes. Therefore W<W0.
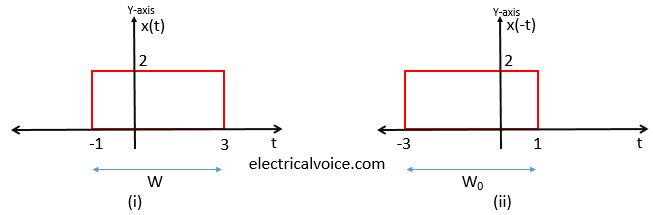
Time Reversal
If the independent variable t is replaced by ‘−t’ , this operation is known as time reversal of the signal about the y-axis or amplitude axis. This can be achieved by taking mirror image of the signal x(t) about y-axis or by rotating x(t) by 180° about y-axis. Hence, time reversal is known as folding or reflection.
Consider a signal x(t) as shown in figure 4(i). The time reversal of this signal can be achieved by taking mirror image in the y-axis as shown in figure 4(ii). During this process, the width of the signal x(t) does not change. Therefore W=W0.