The energy of the continuous-time signal x(t) is given by
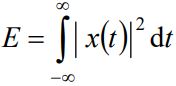
Note: Here x(t) can be a real-valued signal or complex-valued signal.
The energy of the discrete-time signal x(n) is given by
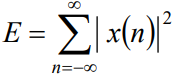
Note: Here x(n) can be a real-valued signal or complex-valued signal.
The power of the continuous-time signal x(t) is given by
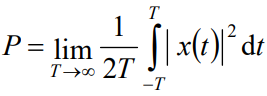
Note: Here x(t) can be a real-valued signal or complex-valued signal.
The power of the discrete-time signal x(n) is given by
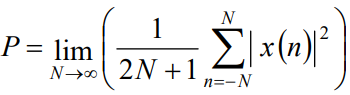
Note: Here x(n) can be a real-valued signal or complex-valued signal.
Note: The signal whose energy is finite and power is zero is known as energy signal. The signal whose power is finite and energy is infinite is known as power signal. You can read more about the energy signal and the power signal here.
Question: Compute energy of the following signal
x(t) = e−t u(t)
Solution. The energy of this signal is
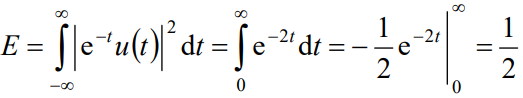
So the energy of the signal x(t) is ½.
Question: Compute energy of the following signal
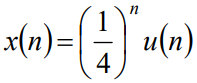
Solution. The energy of this signal is
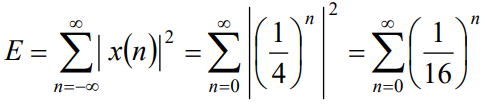
The expression on the right-hand side is a geometric series; hence, we have
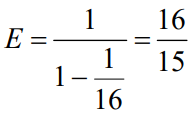
So the energy of the signal x(n) is 16/15.
Question: Compute power of the following signal
![]()
Solution. The power of this signal is
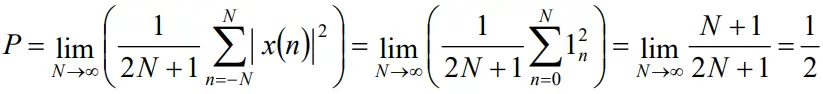
So the power of the signal x(n) is 1/2.

Hello,
Thanks for posting this info.
Question on the energy of x(t)=e^-t * u(t).
While integrating there is integral(e^-2t) = -1/2*(e^-2t).
Where does the 1/2 come from? Shouldn’t it be -2*e^-2t ?