Active Power
The actual amount of power being used, or dissipated, in a circuit is called True power or Active Power or real power. It is measured in watt (W) or kilowatt (kW) or MW. It is symbolized by the capital letter P.
It has been seen that the power is consumed only in resistance.
Reactive Power
The reactive loads such as inductors and capacitors dissipate or consume zero power, yet the fact that they drop voltage and draw current gives the misleading impression that they actually dissipate power. This “phantom or fictitious power” is called reactive power. The reactive power is measured in kilo volt-ampere reactive (kVAR) or MVAR.
The reactive power does not perform any useful work in the circuit. A pure inductor and a pure capacitor do not consume any power since in a half cycle whatever power is received from the source by these components, the same power is returned to the source.
Apparent Power
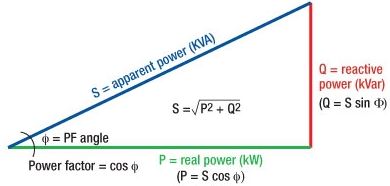
The product of root mean square (RMS) value of voltage and current is known as apparent power. This power is measured in kVA or MVA.
or
The combination of reactive power and true power is called apparent power.
Complex Power
The Complex sum of Real Power (P) and Reactive Power (Q) is known as Complex Power which can be expressed like S = P+jQ and measured in terms of Volt-Amps Reactive (generally in kVAR).
It may also be expressed as S=VI* where “I*” is the conjugate of the complex current I. This current “I” flows through a reactive load Z caused by the Voltage.
Therefore,
True power = voltage x current in phase with the voltage
Reactive power = voltage x current out of phase with the voltage
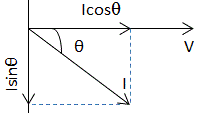
The phasor diagram for an inductive circuit is shown in fig. 1.
The phasor diagram for a capacitive circuit is shown in fig. 2.
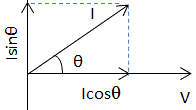
Taking voltage V as a reference, the current I lags behind the voltage V in fig 1 and leads the voltage in fig 2 by a power factor angle θ, respectively. The current I is divided into two components
I Cosθ in phase with the voltage V
I Sinθ is 90° out of phase with the voltage V
Therefore, the following expression shown below gives the active, reactive and apparent power respectively
Active power
P = V x I cosθ = V I cosθ
Reactive power
Q = V x I sinθ = V I sinθ
Apparent power
S = V x I = VI
Active component of the current
The current component which is in phase with the circuit voltage and contributes to the active or true power of the circuit is called active component or wattfull component or in-phase component of the current.
Reactive component of the current
The current component which is in quadrature or 90° out of phase to the circuit voltage and contributes to the reactive power of the circuit is called reactive component of the current.
Power Triangle
True, reactive, and apparent powers are related to one another in trigonometric form as power triangle.