Even signal is a signal which satisfies the relation f(t) = f(−t). Even signal is symmetric about the y-axis. Example: cost.
f(t) = cost
f(−t) = cos(−t) = cost
Hence, f(t) = f(−t)
Odd signal is a signal which satisfies the relation f(t) = −f(−t). Odd signal is symmetric about the origin. Example: sinωt.
f(t) = sint
f(−t) = sin(−t) = −sint
Hence, f(t) = −f(−t)
Properties
The time derivative of even signal gives an odd signal and the time derivative of even signal gives an even signal.

3. The even part of a signal f(t) is given as
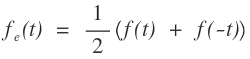
4. The odd part of a signal f(t) is given as
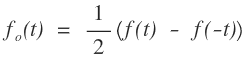
Therefore, f(t) = fe(t) + fo(t)
5. f(t) + f(−t) → It always represents an even signal.
Proof: Let x(t) = f(t) + f(−t)
x(−t) = f(−t) + f(t)
Therefore, x(t) = x(−t)
Hence x(t) is an even signal.
6. f(t) − f(−t) → It always represents an odd signal.
Proof: Let x(t) = f(t) − f(−t)
x(−t) = f(−t) − f(t)
x(−t) = −[−f(−t) + f(t)] = −x(−t)
Therefore, x(t) = −x(−t)
Hence x(t) is an odd signal.
