A XOR gate is a gate that gives a true (1 or HIGH) output when the number of true inputs is odd. An XOR gate is also called exclusive OR gate or EXOR. In a two-input XOR gate, the output is high or true when two inputs are different.
In Boolean expression, the term XOR is represented by the symbol (⊕) and the Boolean expression is represented as Y = A ⊕ B. It is read as “A xor B”.
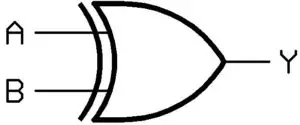
XOR gate symbol
The logic symbol of the XOR gate is shown in figure 1.
XOR gate truth table
The XOR gate truth table for figure 1 is shown below.
| A | B | Y = A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
From XOR gate truth table, it can be concluded that the output will be logical 1 or high when a number of true inputs is odd.
Y = A ⊕ B
Y = ![]() =
= ![]()
The above algebraic expression represent the XOR gate with inputs A and B.
Note:
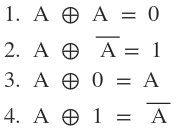
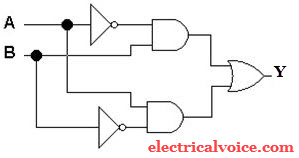
XOR gate using OR, AND, and NOT gate
To produce XOR gate using OR, AND, and NOT gate, the gates are joined together as shown in figure 2.
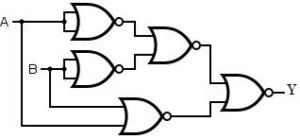
XOR gate using NOR gate
To produce XOR gate using 4 NOR gates, the NOR gates are connected as shown in fig. 3.

To produce XOR gate using 5 NOR gates, the NOR gates are connected as shown in fig. 3.
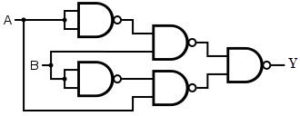
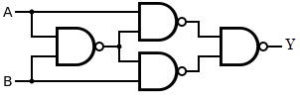
XOR gate using NAND gate
To produce XOR gate using 4 NAND gates, the NAND gates are connected as shown in fig. 5.
To produce XOR gate using 5 NAND gates, the NAND gates are connected as shown in fig. 6.