What is Reciprocity Theorem? Explanation & Limitations

Reciprocity Theorem

In a linear, bilateral time-varying network, the ratio between response to the excitation remains same even after the position of response and excitation are interchanged.

In a very lucid way, we can explain the reciprocity theorem as when the places of voltage and current source in any network are interchanged, the amount or magnitude of the current and voltage flowing in the circuit remains the same.

Note:

1. The Reciprocity Theorem is applicable for both AC and DC Circuits.
2. While applying Reciprocity Theorem, the circuit does not have time varying element.
3. Using Reciprocity Theorem, it is possible to conclude whether a network is linear or non-linear.

Explanation of Reciprocity Theorem

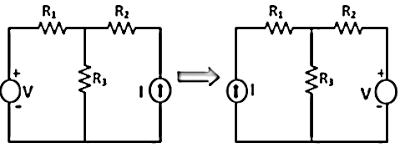
In the above figure, there are three resistances R₁, R₂, and R₃ along with voltage source (V) which is an excitation for the circuit. The response of this circuit is current (I) which is measured through Ammeter (I). According to the Reciprocity Theorem, the voltage source (excitation) and the current response (ammeter) are interchangeable for solving the network. The ratio of response to excitation is constant.

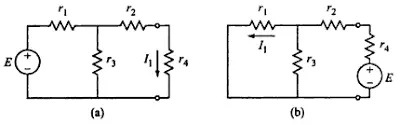
Let us take another example.

Note: To apply the reciprocity theorem, unit of response/excitation should be either mho or ohm while applying theorem circuit should consist of only one independent source.

Limitations of Reciprocity Theorem

1. Not applicable to the circuits consisting of any time varying element.
2. Not applicable to the circuits consisting of the dependent source even it is linear.
3. Not applicable to the circuits consisting of non-linear elements like diode, transistor, etc.