Conjugate symmetric Signal is a signal which satisfies the relation f(t) = f^*(−t). It is also known as even conjugate signal.

Example-1

f(t) = e^jt

f(−t) = e^j(−t)

f^*(−t) = e^(−j)(−t) = e^jt = f(t)

Hence, f(t) = f^*(−t)

Example-2

f(t) = e^jω_ot

f(−t) = e^jω_o(−t)

f^*(−t) = e^{(−j)ω_o(−t)} = e^jω_ot = f(t)

Hence, f(t) = f^*(−t)

As we know that f(t) = e^jω_ot = cosω_ot + j sinω_ot

Real part, f_r(t) = cosω_ot

Imaginary part, f_i(t) = sinω_ot

f_r(−t) = cosω_o(−t) = cosω_ot = f_r(t)

f_i(−t) = sinω_o(−t) = −sinω_ot = −f_i(t)

From above equations, we can conclude that the real part is always even signal and the imaginary part is always odd signal for a conjugate symmetric signal.

Conjugate anti-symmetric Signal is a signal which satisfies the relation f(t) = −f^*(−t). It is also known as odd conjugate signal.

Example-1

f(t) = je^jt

f(−t) = je^j(−t)

f^*(−t) = (−j)e^(−j)(−t) = −je^jt = −f(t)

Hence, f(t) = −f^*(−t)

Example-2

f(t) = je^jω_ot

f(−t) = je^jω_o(−t)

f^*(−t) = (−j)e^{(−j)ω_o(−t)} = −je^jω_ot = −f(t)

Hence, f(t) = −f^*(−t)

As we know that f(t) = je^jω_ot = j[cosω_ot + j sinω_ot]

Real part, f_r(t) = −sinω_ot

Imaginary part, f_i(t) = cosω_ot

f_r(−t) = −sinω_o(−t) = sinω_ot = −f_r(t)

f_i(−t) = cosω_o(−t) = cosω_ot = f_i(t)

From above equations, we can conclude that the real part is always odd signal and the imaginary part is always even signal for a conjugate anti-symmetric signal.

Properties

1. The conjugate symmetric part of a signal f(t) is given as

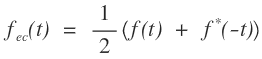
2. The conjugate anti-symmetric part of a signal f(t) is given as

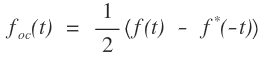
Therefore, f(t) = f_ec(t) + f_oc(t)

3. f(t) + f^*(−t) → It always represents conjugate symmetric signal.

Proof: Let x(t) = f(t) + f^*(−t)

x(−t) = f(−t) + f^*(t)

x^*(−t) = [f(−t) + f^*(t)]^* = f^*(−t) + f(t)

Therefore, x(t) = x^*(−t)

Hence x(t) is conjugate symmetric signal.

4. f(t) − f^*(−t) → It always represents conjugate anti-symmetric signal.

Proof: Let x(t) = f(t) − f^*(−t)

x(−t) = f(−t) − f^*(t)

x^*(−t) = [f(−t) − f^*(t)]^* = f^*(−t) − f(t)

x^*(−t) = −[f(t) − f^*(−t)] = −x(t)

Therefore, x(t) = −x^*(−t)

Hence x(t) is conjugate anti-symmetric signal.