Wheatstone Bridge - Working Principle & Applications

A Wheatstone bridge is used for the accurate measurement of resistance. The Wheatstone bridge works on the principle of null deflection, i.e. the ratio of their resistances are equal, and no current flows through the galvanometer.

Contents show

The general arrangement of the Wheatstone bridge circuit is shown in fig. 1. It is a four arms bridge circuit where arm AB, AD, BC and CD are consisting of electrical resistances P, R, Q and S respectively.

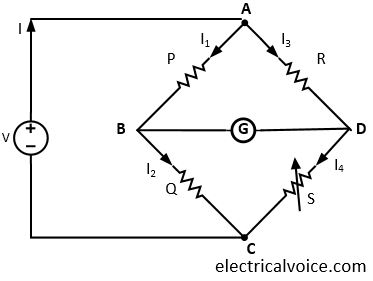
Among these resistances, P and Q are known fixed electrical resistances and these two arms are referred to as ratio arms. A Galvanometer G is connected between terminals B and D.

The voltage source of this Wheatstone bridge is connected to terminals A and C. A variable resistor S is connected between arm CD. The potential at point D can be varied by adjusting the value of the variable resistor S. Let currents I₁ , I₃ , I₂ and I₄ are flowing through the arms AB, AD, BC, and DC, respectively.

Wheatstone bridge Working

If we vary the arm CD resistance S, the value of current I₂ will also be varied as the voltage across A and C is fixed. If we continue to adjust the variable resistance, one situation may come when the voltage drop across the resistor S i.e. (I₄S) becomes exactly equal to the voltage drop across resistor Q i.e. (I₂Q). Thus the potential at point B becomes equal to the potential at point D hence the potential difference between these two points is zero hence current through the galvanometer is zero and there is no deflection in the galvanometer. Therefore, the current flowing in the arm AB and BC are the same i.e. I₁ = I₂. The current flowing in the arm AD and CD are the same i.e. I₃ = I₄.

Note: A Wheatstone bridge is said to be balanced if no current flow through the galvanometer. A Wheatstone bridge is said to be unbalanced if a current flow through the galvanometer. In unbalanced condition, I₁ ≠ I₂and I₃ ≠ I₄.

Now, In balanced Wheatstone bridge

The current flowing through arms AB and BC is

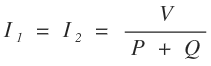
The current flowing through arms AD and DC is

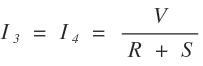
The voltage difference between point B and point C i.e. V_BCis given by

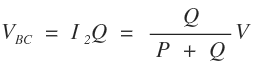
The voltage difference between point D and point C i.e. V_DCis given by

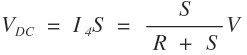
In balanced Wheatstone bridge

V_BC = V_DC

⇒ I₂Q = I₄S

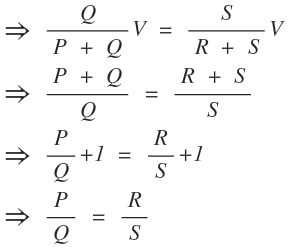
⇒ P S = Q R

In a balanced Wheatstone bridge, the product of opposite side arm resistances is equal i.e. P S = Q R.

From the following equation, the value of R can easily be determined if the values of resistances P, Q and S are known.

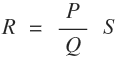
Wheatstone bridge Limitations

A Wheatstone bridge cannot be employed for the measurement of very low resistance as it introduces the error on account of contact resistance, resistance of connecting leads, and thermoelectric EMFs.