AC Bridges are those circuits which are used for the measurement of unknown resistances, capacitance, inductance, frequency and mutual inductance. AC bridges operate with only an AC source. These bridges are very convenient and give the accurate result of the measurement. The construction of these bridge is very simple. Figure 1 shows an AC bridge.
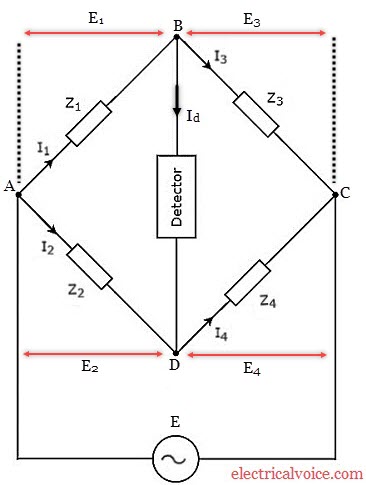
The bridge has four arms (AB, BC, AD, and DC) and four nodes (A, B, C, and D). The source is connected between two nodes and the balance detector is connected between the remaining two nodes. Impedances of 3 arms are known and impedance of remaining arm is unknown. It works on the same principle as the Wheatstone bridge works. The null indication in the detector is obtained when the voltage at node ‘B’ is equal to the voltage at node ‘D’. Due to this, no current will flow through the detector. In such condition, a bridge is said to be balanced.
At the balance condition, the current (Id) through the detector is zero.
Therefore
I1 = I3 …………… (1)
and
I2 = I4 …………… (2)
Then from equation (1) and (2), we have
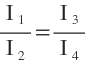…………… (3)
At balance condition, the voltage drop across arm ‘AB’ is equal to the voltage drop across arm ‘AD’.
E1 = E2
I1Z1 = I2Z2
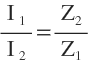…………… (4)
At balance condition, the voltage drop across arm ‘BC’ is equal to the voltage drop across arm ‘DC’.
E3 = E4
I3Z3 = I4Z4
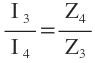…………… (5)
From equation (1), it can be seen that equations (4) and equation (5) are equal and we have
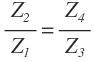
hence
…………… (6)
Therefore, the products of impedances of opposite arms are equal.
Note: All the above quantities are in phasor form.
In equation (6), writing impedances in polar form, we have
…………… (7)
From equation (7), we have
…………… (8)
and
…………… (9)
It can be concluded that for a bridge to be balanced, both magnitude and phase are required to be equal as seen in equations (8) and (9).
If any of the two equations (8) or (9) is not satisfied then the bridge is said to be unbalanced.
Sources use in AC bridge
1. Low-frequency source
2. High-frequency source
Detectors use in AC bridge
1. Vibrational galvanometer (5 Hz to 1000 Hz)
2. Headphone/Telephone detector (250 Hz to 4 kHz)
3. Tuned amplifier detector (10 Hz to 10 kHz)
4. CRO (for high-frequency)
Applications of AC bridges
1. It is used for the measurement of inductances. The following AC bridges are used for the measurement of self-inductance of the coil.
- Maxwell inductance bridge
- Maxwell inductance-capacitance bridge
- Hay’s bridge
- Owen’s bridge
- Anderson’s bridge
2. It is used for the measurement of capacitances. The following AC bridges are used for the measurement of capacitance.
- De-sauty’s bridge
- Schering bridge
3. It is used for the measurement of frequency. The following AC bridges are used for the measurement of frequency.
- Wien’s bridge
4. It is used for the measurement of the dissipation factor.
5. It is used in providing phase-shifting and a feedback path to the oscillator.
Questions & Answers
Question. The four impedances of an ac bridge as shown in figure 1 are Z1 = 500∠40° Ω, Z2 = 100∠90° Ω, Z3 = 45∠20° Ω, Z4 = 30∠30° Ω. Find out whether the bridge is balanced or not.
Solution. As we know in polar co-ordinate system representation, the bridge balance conditions are
and
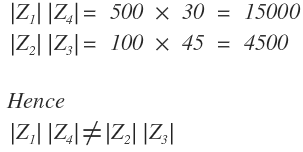
θ1 + θ4 = 40° + 30° = 70°
θ2 + θ3 = 90° + 20° = 110°
Hence
θ1 + θ4 ≠ θ2 + θ3
Therefore, the bridge is unbalanced.
