State Space Representation of a System

The control system analysis fails for multiple-input multiple-output (MIMO) systems and the systems initially not at rest by using transfer function approach. The use of the state-space approach for the analysis of control systems enables to overcome the shortcomings of the transfer function approach.

Contents show

State

The state of a dynamic system is the smallest state of variables (called as state variables) such that the knowledge of these variables at the time ‘t_o‘ together with the input t > t_o determines the unique behaviour of the system for t > t_o and this t_o is normally taken as zero.

This amount of information is generally a set of variables which are the values from inside the system that can change over time. for example in an electric circuit containing RLC network as shown in the figure.

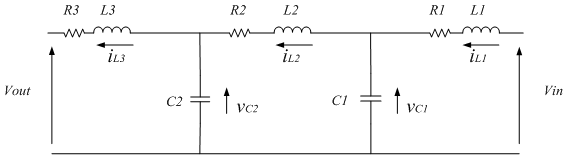
Initial inductor current i.e. i_L(0) and

initial capacitor voltage i.e. v_c(0) can be state variables.

On applying input i.e. closing the switch, these state variables will change and hence the state of the network at time ‘t’ will be i_L(t) and v_c(t).

In general, the state of the system is represented by a set of the equation called as state equations. The general form of state equation is as follows

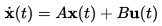………………. (1)

The output of system can be represented by the output equation y(t)

y(t) = C x(t) + D u(t) ………………. (2)

where x denotes the state variable

u denotes the input variable

y denotes the output variable.

A is called system Matrix

B is called the controlled Matrix

C is called the output matrix

D is called the feed forward matrix

Equations (1) and (2) represent the state model of the system and are collectively called state space equation.

Note: The requirement in choosing this state variable is that they should be linearly independent* and that minimum^# number of them should be chosen.

# decided by the order of the differential equation describing the system.