Kalman Filter | Algorithm & Applications

The Kalman filter is a recursive state space model based estimation algorithm. In other words, it is an optimal recursive data processing algorithm. Kalman filter is also called as the Predictor-Corrector algorithm.

This filter is named after Rudolph E. Kalman, who in 1960 published his famous paper describing a recursive solution to the discrete data linear filtering problem.

Kalman filter processes all available measurements regardless of their precision to estimate the current value of the variables of interest with the use of

• knowledge of the system and measurement device dynamics.
• statistical description of the system noises measurement errors and uncertainty in the dynamic models.
• Any available information about initial conditions of variables of interest.

Linear Kalman Filter

It works with two assumptions i.e.

1. The system is linear
2. The system and measurement noise are white Gaussian noise.

White Noise

1. Noise value is not correlated in time. Prediction is not possible.
2. The noise has equal power at all frequencies.

Kalman filter algorithm was basically developed for single dimensional and real valued signals which are associated with the linear systems assuming the system is corrupted with linear additive white Gaussian noise.

The Kalman filter addresses the general problem of trying to estimate the state x ∈ ℜⁿ of a discrete-time controlled process that is governed by the linear difference equation.

x_k = Ax_{k – 1} + Bu_{k – 1} + w_{k – 1}

with a measurement z that is

z_k = Hx_k + v_k

The random variables w_k and v_k represent the process noise and measurement noise respectively.

The n × n matrix A in the previous difference equation relates the state at the previous time step k-1 to the state at the current step k, in the absence of either a driving function or process noise.

The n × 1 matrix B relates the optional control input u to the state x.

The m × n matrix H in the measurement equation relates the state to the measurement z_k.

The Computational Origins of the Filter:

We define   be our apriori state estimate at step k given knowledge of the process prior to step k, and    to be our aposteriori state estimate at step k given measurement z_k.

We can then define apriori and aposteriori estimate errors as

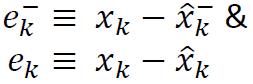
The apriori estimate error covariance is then

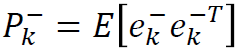
the a posteriori estimate error covariance is

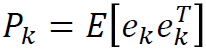
The posteriori state estimate  is written as a linear combination of an apriori estimateand a weighted difference between an actual measurement z_k & a measurement prediction H.

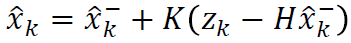
The difference (−) is called the measurement innovation, or the residual.

The n x m matrix K is chosen to be the gain or blending factor that minimizes the aposteriori error covariance.

Substituting in e and e  in P_k , and performing minimization, we get

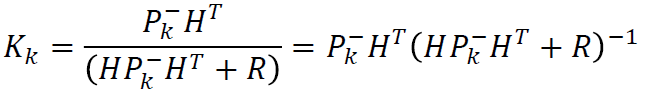
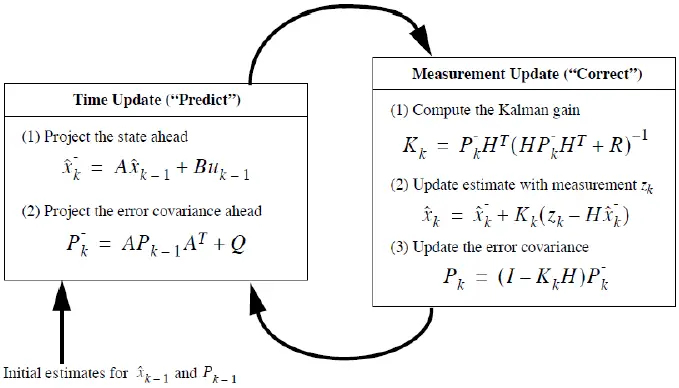
Kalman filter algorithm

1. The Kalman filter estimates a process by using a form of feedback control: the filter estimates the process state at some time and then obtains feedback in the form of (noisy) measurements.

2. As such, the equations for the Kalman filter fall into two groups: time update equations and measurement update equations.

3. The time update equations are responsible for projecting forward (in time) the current state and error covariance estimates to obtain the apriori estimates for the next time step.

4. The measurement update equations are responsible for the feedback i.e. for incorporating a new measurement into the apriori estimate to obtain an improved a posteriori estimate.

5. The time update equations can also be thought of as predictor equations, while the measurement update equations can be thought of as corrector equations.

6. The final estimation algorithm resembles that of a predictor-corrector algorithm.

Discrete Kalman filter time update equations:

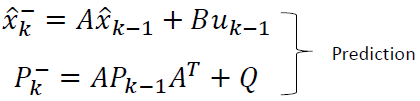
Discrete Kalman filter measurement update equations:

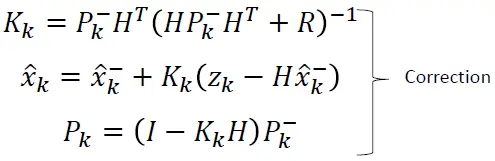
A complete picture of the operation of the Kalman filter is shown below.

 

What are the properties of Kalman Filter?

Answer. The properties of Kalman filter are as follows

1. Kalman filter is a time-varying filter as Kalman gain changes with n.
2. The filter is very powerful in several aspects: it supports estimations of past, present, and even future states, and it can do so even when the precise nature of the modeled system is unknown.
3. In the Kalman filter, prediction acts like the prior information about the state at time n before we observe the data at time n.

What are the limitations of Kalman filter?

Answer. Kalman filter assumes an approximate solution, describe the deviations from the reference by linear equations. Kalman filter has issues of divergence also.

When the error covariance matrix P_k computed by the Kalman filter becomes unjustifiably small compared to the actual error in the estimate. Also, the gain matrix becomes too small and a new measurement is given very small weightage. So, plant model becomes more important. There is an effect on the accuracy of the estimate. To overcome this problem an Extended Kalman Filter is used for non-linear applications.

What are the Kalman Filter Applications?

Answer. The applications of Kalman filter are as follows

1. Tracking objects (e.g., missiles, faces, heads, hands)
2. Fitting Bezier patches to (noisy, moving, …) point data
3. Economics
4. Navigation
5. Many computer vision applications
   – Stabilizing depth measurements
   – Feature tracking
   – Cluster tracking
   – Fusing data from radar, laser scanner and
   – Stereo-cameras for depth and velocity measurements