In the previous article, we had learned about Kalman filter. As Kalman filter assumes linear system but finds greatest applications in non-linear systems. Kalman filter assumes an approximate solution, describe the deviations from the reference by linear equations. Kalman filter has issues of divergence also.
When the error covariance matrix Pk computed by the Kalman filter becomes unjustifiably small compared to the actual error in the estimate. Also, the gain matrix becomes too small and a new measurement is given very small weightage. So, plant model becomes more important. There is an effect on the accuracy of the estimate. To overcome this problem an Extended Kalman Filter is used for non-linear applications.
An Extended Kalman filter is used if the process to be estimated and (or) the measurement related to the process is non-linear.
The extended Kalman filter linearizes the non-linear system at each stage by employing the best estimates of the state vector as the reference values.
Necessary and sufficient conditions for extended Kalman filter: The error in the estimate is orthogonal to the measurement data.
Here
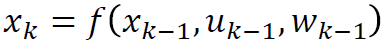
with measurement z that is
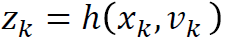
Similar to the Kalman filter, the time and measurement equations for Extended Kalman Filter can be written as below:
Extended Kalman Filter time update equations:
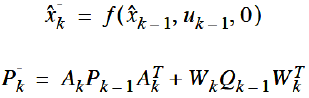
Extended Kalman Filter measurement update equations:
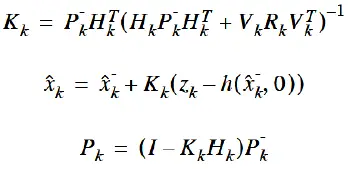

A complete picture of the operation of the Extended Kalman filter is shown in the figure below.

