Inductor MCQ | Inductance MCQ

1. What determines the inductance of a coil?

  1. the core material, the number of turns used to wind the core and the frequency of the current through the coil.
  2. the core material, the core diameter, the length of the coil and the number of turns of wire used to wind the coil.
  3. the core diameter, the number of turns of wire used to wind the coil and the type of metal used for the wire.
  4. the core material, the core diameter, the length of the coil and whether the coil is mounted horizontally or vertically.
Answer
Answer. b

2. Energy stored in an inductor is in the form of

  1. current
  2. magnetic field
  3. electric field
  4. charge
Answer
Answer. b

3. The inductance of a solenoid of 10 turns is 5 mH. If the number of turns is doubled, the inductance of the coil will be

  1. 10 mH
  2. 20 mH
  3. 30 mH
  4. 5 mH
Answer
Answer. a

4. Lower the self-inductance of a coil

  1. more will be the weber turns
  2. more will be the emf induced
  3. lesser will be the flux produced by it
  4. smaller the delay in establishing steady current through is
Answer
Answer. d

5. The mutual inductance between two closely coupled coils is 1H. If the turns of one coil is decreased to half and those of the other is doubled, the new value of the mutual inductance would be

  1. 1/4 H
  2. 1 H
  3. 2 H
  4. 1/2 H
Answer
Answer. b

6. The mutual inductance between two coupled coils is 10 mH. If the turns in one coil are doubled and that in the other are halved then the mutual inductance will be

  1. 10 mH
  2. 5 mH
  3. 20 mH
  4. 15 mH
Answer
Answer. c

7. The coefficient of coupling between two coils is 0 to 0.45. The first coil has an inductance of 75 mH and the second coil has an inductance of 105 mH. What is the mutual inductance between the coils?

  1. 3.54 mH
  2. 7.88 mH
  3. 39.9 mH
  4. 189.3 mH
Answer
Answer. c

8. The mutual inductance between two coupled coils is 10 mH. If the turns in one coil are doubled and that in the other are halved, then the mutual inductance will be

  1. 5 mH
  2. 10 mH
  3. 14 mH
  4. 20 mH
Answer
Answer. b

9. Given two coupled inductors L1 and L2, their mutual inductance M satisfies

Answer
Answer. d

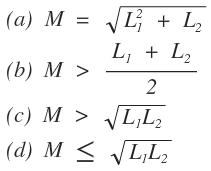
10. When two coils having self-inductances of L1 and L2 are coupled through a mutual inductance M, the coefficient of coupling, K is given by

Answer
Answer. b

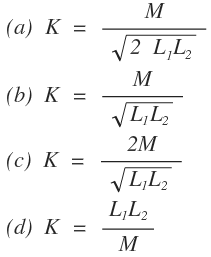
11. The overall inductance of two coils connected in series, with mutual inductance aiding self-inductance is L1; with mutual inductance opposing self-inductance the overall inductance is L2. The mutual inductance M is given by

Answer
Answer. c

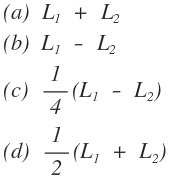
12. Two coupled coils connected in series have an equivalent inductance of 16 mH or 8 mH depending on the interconnection. Then the mutual inductance M between the coils is

  1. 12 mH
  2. 8 mH
  3. 4 mH
  4. 2 mH
Answer
Answer. d

13. Two coils having self-inductance of 10 mH and 15 mH and effective inductance of 40 mH, when connected in series aiding. What will be the equivalent inductance if we connect them in series opposing?

  1. 20 mH
  2. 10 mH
  3. 5 mH
  4. zero
Answer
Answer. b

14. The coupling between two magnetically coupled coils is said to be ideal if the coefficient of coupling is

  1. zero
  2. 0.1
  3. 1
  4. 2
Answer
Answer. c

15. Two inductive coils with self inductance L1 and L2 are magnetically coupled in series opposing and in parallel aiding respectively. The mutual inductance between the coils in the two cases are respectively

Answer
Answer. c

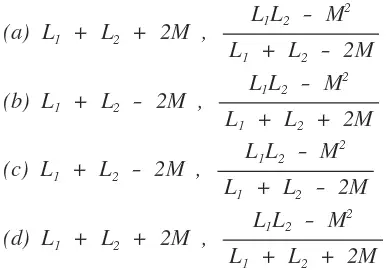
16. Two coupled coils with L1 = L2 = 0.6 H have a coupling coefficient of K = 0.8. The turn ratio (N1/N2) is

  1. 4
  2. 2
  3. 1
  4. 0.5
Answer
Answer. c

17. In case all the flux from the current in coil 1 links with coil 2, the coefficient of coupling will be

  1. 2.0
  2. 1.0
  3. 0.5
  4. zero
Answer
Answer. b

18. Two coils are coupled in such a way that the mutual inductance between them is 16 mH, if the inductances of the coils are 20 mH and 80 mH respectively, the coefficient of coupling is

  1. 0.01
  2. 0.4
  3. 0.1
  4. 0.0025
Answer
Answer. b

19. Two identical coils of negligible resistance, when connected in series across a 50 Hz fixed voltage source, draw a current of 10 A. When the terminals of one of the coils are reversed, the current drawn is 8 A. The coefficient of coupling between the two coils is

  1. 1/100
  2. 1/9
  3. 4/10
  4. 8/10
Answer
Answer. b

20. Two inductors have self inductances of 9 mH and 25 mH. The mutual inductance between the two is 12 mH. The coefficient of inductive coupling between the two inductors is

  1. 18.75
  2. 0.25
  3. 0.8
  4. 1.25
Answer
Answer. c

21. Inductance has the dimension of

  1. flux/current
  2. flux/length
  3. (voltage)2/current
  4. none of these
Answer
Answer. a

22. The mutual inductance between two coils having self inductances 3 henry and 12 henry and coupling coefficient 0.85 is

  1. 12.75 henry
  2. 5.1 henry
  3. 0.425 henry
  4. 1.7 henry
Answer
Answer. b

23. A 100 turn coil has an inductance of 6 mH. If the number of turns is increased to 200, all other quantities remaining the same, the inductance will be

  1. 24 mH
  2. 12 mH
  3. 3 mH
  4. none of these
Answer
Answer. a

24. Which is known as electrical inertia?

  1. R
  2. L
  3. C
  4. none of the above
Answer
Answer. b

25. The number of turns and length of a coil are increased two times. Its self-inductance

  1. becomes halved
  2. quadruples
  3. remains unaffected
  4. doubles
Answer
Answer. d

26. What is that property of a coil called under which if there is a change in the current flowing through it, a voltage gets induced in the coil itself as well as the neighbouring circuit?

  1. resistivity
  2. inductance
  3. charging
  4. none of the above
Answer
Answer. b

27. Which one of the following is a valid value of coefficient of coupling between two inductors?

  1. 1.414
  2. 0.9
  3. 1.732
  4. 17.32
Answer
Answer. b

28. Two coils have self-inductance L1 and L2 henry respectively. If the two coils are connected in series and the mutual inductance between them is M henry, the value of maximum resultant inductance of the combination will be

  1. L1 + L2 + M
  2. L1 + L2 + 2M
  3. L1 + L2 – M
  4. L1 + L2 – 2M
Answer
Answer. b

29. What is the effect of the high value of self-inductance of a coil?

  1. lower emf will be induced
  2. greater delay in establishing steady current
  3. weber turns will be lesser
  4. greater flux produced
Answer
Answer. b

30. Three inductors each of 60 mH are connected in delta. The value of inductance of each arm of the equivalent star connection is

  1. 10 mH
  2. 15 mH
  3. 20 mH
  4. 30 mH
Answer
Answer. c
Pages: 1 2 3