Here in this tutorial, we are going to learn how to find the inverse of a matrix in MATLAB. First of all, see what is the syntax of matrix inverse in MATLAB.
Syntax
A = inv(B)
where B is the square matrix and A is the inverse of matrix B.
Let us take a few examples to see how you find matrix inverse easily.
Example-1: Find the inverse of the following 2 x 2 matrix
$\begin{pmatrix} 2 & 3 \\ 5 & 7 \end{pmatrix}$
MATLAB code
B = [2 3; 5 7]; A = inv(B)
Output
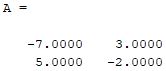
Explanation
First of all, we write the code for the matrix as B = [2 3; 5 7]. In the second step, we write code for matrix inverse as A = inv(B). Here A is the inverse of 2 x 2 matrix.
Example-2: Find the inverse of the following 3 x 3 matrix
$\left( \begin{matrix} 5 & 7 & 9 \\ 4 & 1 & 8 \\ 5 & 2 & 4 \end{matrix} \right)$
MATLAB code
B = [5 7 9; 4 1 8; 5 2 4]; A = inv(B)
Output
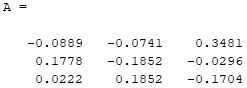
Explanation
First of all, we write the code for the matrix as B = [5 7 9; 4 1 8; 5 2 4]. In the second step, we write code for matrix inverse as A = inv(B). Here A is the inverse of 3 x 3 matrix.
Example-3: Find the inverse of the following 4 x 4 matrix
$\left( \begin{matrix} 5 & 7 & 9 & 11 \\ 4 & 1 & 8 & 7 \\ 5 & 2 & 4 & 9 \\ 4 & 8 & 7 & 11\end{matrix} \right)$
MATLAB code
B = [5 7 9 11; 4 1 8 7; 5 2 4 9; 4 8 7 11]; A = inv(B)
Output
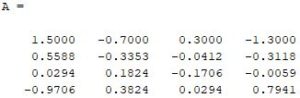
Explanation
First of all, we write the code for the matrix as B = [5 7 9 11; 4 1 8 7; 5 2 4 9; 4 8 7 11]. In the second step, we write code for matrix inverse as A = inv(B). Here A is the inverse of 4 x 4 matrix.
So in this tutorial we see how can we find the inverse of matrix easily in MATLAB.
