Economic Load Dispatch MCQs

1. Consider the economic dispatch problem for a power plant having two generating units. The fuel costs in Rs/MWh along with the generation limits for the two units are given below:

$C_1(P_1)=0.01P_{1}^{2}+30P_1+10$;    100MW≤P₁≤150MW
$C_2(P_2)=0.05P_{2}^{2}+10P_2+10$;  100MW≤P₂≤180MW

The incremental cost (in Rs/MWh) of the power plant when it supplies 200 MW is _____.

1. 20
2. 22
3. 21
4. 24

2. The incremental costs (in Rupees/MWh) of operating two generating units are functions of their respective powers P₁ and P₂ in MW, and are given by

\[\frac{\mathrm{d} C_1}{\mathrm{d} P_1}=0.2P_1+50\]

\[\frac{\mathrm{d} C_2}{\mathrm{d} P_2}=0.24P_2+40\]

Where

20MW ≤ P₁ ≤ 150 MW
20MW ≤ P₂ ≤ 150MW

For a certain load demand, P₁ and P₂ have been chosen such that $\frac{\mathrm{d} C_1}{\mathrm{d} P_1}$ = 76 Rs/MWh and $\frac{\mathrm{d} C_2}{\mathrm{d} P_2}$ = 68.8 Rs/MWh. If the generations are rescheduled to minimize the total cost, then P₂ is _____________.

1. 135 MW
2. 126.24 MW
3. 144 MW
4. 136.36 MW

3. The fuel cost functions of the two power plants are:

Plant P₁: $C_1=0.05P_{1}^{2}+AP_1+B$
Plant P₂: $C_2=0.10P_{2}^{2}+3AP_2+2B$

where, P₁ and P₂ are the generated powers of two plants, and A and B are the constants. If the two plants optimally share 1000 MW load at an incremental fuel cost of 100 Rs/MWh, the ratio of load shared by plants P₁ and P₂ is

1. 1:4
2. 2:3
3. 3:2
4. 4:1

4. The figure shows a two-generator system supplying a load of P_D = 40 MW, connected at bus 2.

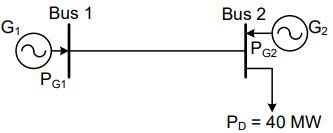
The fuel cost of generators G₁ and G₂ are:
C₁(P_G1) = 10,000 Rs/MWh and C₂(P_G2) = 12,500 Rs/MWh

and the loss in the line is $P_{loss(pu)}=0.5P_{G1(pu)}^{2}$, where the loss coefficient is specified in pu on a 100 MVA base. The most economic power generation schedule in MW is

1. P_G1 = 20, P_G2 = 22
2. P_G1 = 22, P_G2 = 20
3. P_G1 = 20, P_G2 = 20
4. P_G1 = 0, P_G2 = 40

5. A load center of 120 MW derives power from two power stations connected by 220 kV transmission lines of 25 km and 75 km as shown in the figure below. The three generators G1, G₂ and G₃ are of 100 MW capacity each and have identical fuel cost characteristics. The minimum loss generation schedule for supplying the 120 MW load is

a. P1 = 80 MW + losses
P2 = 20 MW
P3 = 20 MW

b. P1 = 60 MW
P2 = 30 MW + losses
P3 = 30 MW

c. P1 = 40 MW
P2 = 40 MW
P3 = 40 MW + losses

d. P1 = 30 MW + losses
P2 = 45 MW
P3 = 45 MW

6. A lossless power system has to serve a load of 250 MW. There are two generators (G₁ and G₂) in the system with cost curves C₁ and C₂; respectively defined as follows:

$C_1(P_1)=0.055P_{1}^{2}+P_1$
$C_2(P_2)=0.03P_{2}^{2}+3P_2$

where P₁ and P₂ are the MW injections from generator G₁ and G₂ respectively. Thus, the minimum cost dispatch will be

1. P₁ = 250 MW and P₂ = 0 MW
2. P₁ = 150 MW and P₂ = 100 MW
3. P₁ = 100 MW and P₂ = 150 MW
4. P₁ = 0 MW and P₂ = 250 MW

7. The incremental cost characteristic of two generators delivering 200 MW are as follows:

\[\frac{\mathrm{d} F_1}{\mathrm{d} P_1}=0.1P_1+20\]

\[\frac{\mathrm{d} F_2}{\mathrm{d} P_2}=0.2P_2+16\]

For economic operation, the generation P₁ and P₂ should be

1. P₁ = P₂ = 100 MW
2. P₁ = 80 MW and P₂ = 120 MW
3. P₁ = 200 MW and P₂ = 0 MW
4. P₁ = 120 MW and P₂ = 80 MW

8. In power system, the fuel inputs per hour of plants 1 and 2 are given as

$F_1=0.20P_{1}^{2}+30P_1+100$ Rs. per hour
$F_2=0.25P_{2}^{2}+40P_2+80$ Rs. per hour

The limits of generators are

20 MW ≤P₁≤ 80MW
40 MW ≤P₂≤ 200MW

Find the economic operating schedule of generation, if the load demand is 130 MW, neglecting transmission losses.

1. P₁ = P₂ = 65 MW
2. P₁ = 80 MW and P₂ = 50 MW
3. P₁ = 130 MW and P₂ = 0 MW
4. P₁ = 100 MW and P₂ = 30 MW

9. A power system has two generators with the following cost curves.

$F_1=0.006P_{1}^{2}+8P_1+350$ Thousand Rs. per hour
$F_2=0.006P_{2}^{2}+7P_2+400$ Thousand Rs. per hour

The limits of generators are

100 MW ≤P₁≤ 650 MW
50 MW ≤P₂≤ 500 MW

A load demand of 600 MW is supplied by the generators in an optimal manner. Neglecting losses in the transmission network, determine the optimal generation of each generator.

10. Incremental fuel costs (in some appropriate unit) for a power plant consisting of three generating units are

$IC_1=20+0.3P_1$, $IC_2=30+0.4P_2$, $IC_3=30$, where P₁ is the power in MW generated by unit i, for i = 1, 2 and 3.

Assume that all three units are operating all the time. Minimum and maximum loads on each unit are 50 MW and 300 MW respectively. If the plant is operating on economic load dispatch to supply the total power demand of 700 MW, the power generated by each unit is

1. P₁ = 242.86 MW; P₂ = 157.14 MW; and P₃ = 300 MW
2. P₁ = 157.14 MW; P₂ = 242.86 MW; and P₃ = 300 MW
3. P₁ = 300 MW; P₂ = 300 MW; and P₃ = 100 MW
4. P₁ = 233.3 MW; P₂ = 233.3 MW; and P₃ = 233.4 MW

11. A load centre is at an equidistant from the two thermal generating stations G₁ and G₂ as shown in the figure. The fuel cost characteristics of the generating stations are given by

$F_1=cP_{1}^{2}+bP_1+a$
$F_2=2cP_{2}^{2}+bP_2+a$

where P₁ and P₂ are the generations in MW of G1 and G2, respectively. For most economic generation to meet 300 MW of load, P₁ and P₂, respectively are

1. 150, 150
2. 100, 200
3. 200, 100
4. 175, 125

12. The incremental cost curves in Rs/ MWhr for two generators supplying a common load of 700 MW are shown in the figures. The maximum and minimum generation limits are also indicated. The optimum generation schedule is:

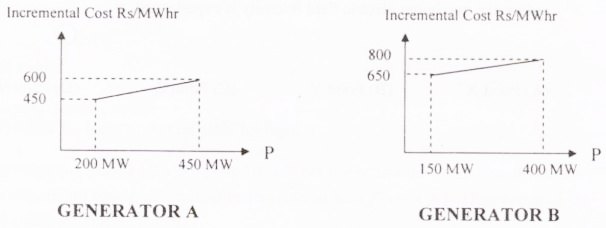
1. Generator A: 400 MW, Generator B: 300 MW
2. Generator A: 350 MW, Generator B: 350 MW
3. Generator A: 450 MW, Generator B: 250 MW
4. Generator A: 425 MW, Generator B: 275 MW

13. A lossless power system has two generators (G₁ and G₂) and total load to be served is 200 MW. The respective cost curves C₁ and C₂; defined as

$C_1=0.01P_{1}^{2}+P_1$
$C_2=0.02P_{2}^{2}+5P_2$

Assume the minimum loading on any generator to be 30 MW. The most economical loads P₁ and P₂ for the two generators G₁ and G₂ are respectively

1. P₁ = 170 MW and P₂ = 100 MW
2. P₁ = 200 MW and P₂ = 100 MW
3. P₁ = 170 MW and P₂ = 30 MW
4. P₁ = 200 MW and P₂ = 30 MW

14. The loss formula coefficient matrix for a two-plant system is given by

\[B=\begin{bmatrix} 0.001 & -0.0001\\ -0.0001 & 0.0013 \end{bmatrix}MW^{-1}\]

The economic schedule for a certain load is given as

P₁ = 150 MW and P₂ = 275 MW

What is the penalty factor for plant 1 for this condition?

1. 1.324
2. 1.515
3. 1.575
4. 1.721

15. The incremental fuel costs of two units A and B of a power station are

\[\frac{\mathrm{d} F_A}{\mathrm{d} P_A}=0.4P_A+400\]

\[\frac{\mathrm{d} F_B}{\mathrm{d} P_B}=0.48P_B+320\]

For the minimum cost of generation of a total load of 900 MW, the generation allocation for A and B units respectively are

1. 200 MW and 700 MW
2. 300 MW and 600 MW
3. 400 MW and 500 MW
4. 500 MW and 400 MW

16. The incremental fuel costs for two generating units G₁ and G₂ are given by

$IC_1=25+0.2P_1$, and $IC_2=32+0.2P_2$, where P₁ and P₂ are real power generated by the units. The economic allocation for a total load of 250 MW, neglecting transmission loss, is given by

1. P₁ = 142.5 MW; P₂ = 107.5 MW
2. P₁ = 109.75 MW; P₂ = 114.25 MW
3. P₁ = 125 MW; P₂ = 125 MW
4. P₁ = 100 MW; P₂ = 150 MW

17. Two generating stations connected to a load centre having capacity of 50 MVA and 75 MVA deliver 100 MW to the load. The incremental cost of plant 1 is $IC_1=15+0.15P_1$ and that of the plant 2 is $IC_2=18+0.15P_2$. What are the values of P₁ and P₂ , respectively?

1. 60 MW and 40 MW
2. 50 MW each
3. 72 MW and 28 MW
4. 30 MW and 70 MW

18. Two power plants interconnected by a tie-line as shown in the below figure have loss formula coefficient B₁₁ = 10^-3 MW^-1. Power is being dispatched economically with plant ‘1’ as 100 MW and plant ‘2’ as 125 MW. The penalty factors for plants 1 and 2 are respectively

 

1. 1 and 1.25
2. 1.25 and 1
3. 1 and 0
4. 0 and 1

19. Calculate the power loss, if power generated by two plants are P₁ = 50 MW and P₂ = 40 MW and the loss coefficients are B₁₁ = 0.001, B₂₂ = 0.0025 and B₁₂ = −0.0005.

1. 4.5 MW
2. 5.5 MW
3. 6.5 MW
4. 8.5 MW