Voltmeter–Ammeter Method for Measuring Medium Resistances

In this article, we’ll learn voltmeter-ammeter method for the measurement of the medium resistances. As the name of the method suggests, we are having ammeter and voltmeter in this method to measure the resistance of the resistor.

There are two possible connections while measuring the medium resistances by this method. We’ll discuss both the connections briefly. The common thing in both cases is that we need to take voltmeter and ammeter reading.

Let the reading of voltmeter and ammeter be ‘V’ and ‘I’ respectively. So, the measured resistance (R_m) will be given by the formula,

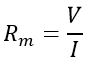
There is a difference between a measured value and true value of the resistor. To achieve the true value of resistance the ammeter resistance should become zero and voltmeter resistance should become infinite, but these are ideal conditions which are practically not possible to achieve. Hence there will be a deviation in measured value and true value and we will find the percentage error for the same.

voltmeter-ammeter method Case-1

[To be used when measuring resistances are high]

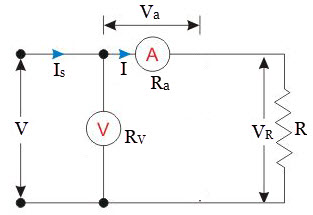
In the above circuit (Fig.1), ammeter measures the true value of current flowing through resistance but voltmeter does not measure the true value of the voltage across the resistance.

Here, voltmeter indicates the sum of the voltage across resistance and ammeter.

Let voltage of voltmeter be V.
Let voltage across ammeter be represented by V_a.
Let voltage across resistance be represented by V_R.

Then we get,

    —————- (1)

The voltage across resistance (V_R) is given by,

            —————- (2)

Now let R_a be the resistance of ammeter.

Therefore, the voltage across the ammeter,

Now measured value (R_m1) of the resistance,

Substituting the value of V from equation (1)

Substituting the value of V_R and V_a from equation (2) and equation (3)

Taking out I common we get,

Cancelling out I, we get,

Therefore, the true value of resistance (R),

Taking out R_m1 common from the equation,

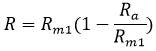
Hence the measured value of resistance is higher than the true value. It is also clear from the above equation that the true value is equal to the measured value only if the ammeter resistance is zero.

Relative error,

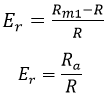
It is clear from the above equation that the error (E_r) will have a small value if the value of the measuring resistance (R) is large as compared to the internal resistance of the ammeter.

Therefore, this circuit should be used when measuring resistances are high.

voltmeter-ammeter method Case-2

[To be used when measuring resistances are low]

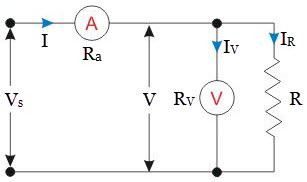
In this circuit (Fig.2), the voltmeter measures the true value of the voltage across the measuring resistance, but the ammeter does not measure the true value of the current flowing through the resistance.

The current through the ammeter is the sum of the current through the voltmeter and resistance.

Let current through ammeter be I.
Let current through voltmeter be represented by I_V.
Let current through resistance be represented by I_R.

Then we get,

   ——————– (4)

Current across resistance (I_R) is given by,

      ——————– (5)

Now let R_v be the resistance of voltmeter.

Therefore, the current through the voltmeter,

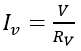    ——————— (6)

Now measured value (R_m2) of the resistance,

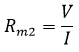
Substituting the value of I from equation (4)

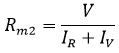
Substituting the value of I_R and I_V from equations (5) and equation (6)

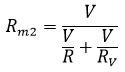
Taking out V common we get,

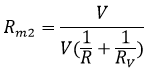
Cancelling out V we get arranging values we get,

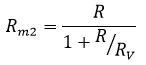
Therefore, the true value of resistance (R),

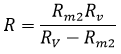
Taking out R_m2 common from the equation,

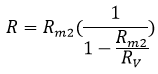
Therefore, the true value of Resistance will only be equal to the measured value if the value of resistance of voltmeter (R_V) is infinite.

Now if we assume that the value of resistance of voltmeter (R_V) is large as compared to the Resistance to be measured R, then R_V >>> R_m2

Therefore, is small

We know that,

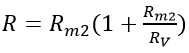
Thus, the measured value of the resistance is smaller than the true value.

Relative Error,

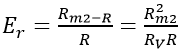
The value of R_m2 is approximately equal to R.

Therefore,

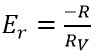
It can be observed from the above equation that the relative error will be low if the resistance under measurement is very small as compared to the internal resistance of the voltmeter (R_V).

Therefore, this circuit should be used when the measuring values of resistances are low.

Note:

1. The voltmeter ammeter method for Case 1 and Case 2 are simple method but it is not an accurate method. The error in the value of Resistance depends on the accuracy of ammeter and voltmeter.

2. Voltmeter-ammeter method is very useful where high accuracy is not required.

3. The suitability of Case 1 or Case 2 depends on the value of Resistance to be measured.

Author:

Adarsh Chauhan

Vidyalankar Institute of Technology
Mumbai