Boolean algebra is a set of rules which are used to simplify the given logic expression without changing its original functionality. So in this article, we are going to learn about Boolean algebra. The Boolean algebra was invented by George Boole; an English mathematician who helped in establishing modern symbolic logic and whose algebra of logic, now popularly known as Boolean algebra. Other names for boolean algebra are binary algebra and logical algebra.
We can also say that Boolean algebra is mathematics which is used to analyze circuits containing gates. Boolean algebra holds real importance in designing the circuits as these help in reducing the number of gates required thus making your system compact and reduce the overall production cost.
Boolean algebra has some rules and laws which we need to know to apply them to reduce boolean expression. But before that let us understand where the Boolean algebra can be used.
Boolean algebra can be used when number of variables are less in a boolean expression. For example: F = A.B+A.B’. Here only two variables are present, so this function can be easily solved by using rules and laws of Boolean algebra.
But in cases where the function contains more than three variables, it is better not to use Boolean algebra as the equation becomes long and you may sometimes end up with the wrong answer. For variables more than three, there are other techniques to simply which are simple like K-map about which you may learn later.
Note: The variables in Boolean algebra can have values either “0” or “1” but expression can have an infinite number of variables. So, after learning where we can use Boolean algebra let us learn about Boolean algebra laws.
The important rules and laws in Boolean algebra are as follows.
1. Rules associated with Complement operation
The complement is the inverse of a variable and is indicated by a ‘ over a variable or a bar over a variable. For example, the complement of the variable A is A’.
The complement of 0 is 1
The complement of 1 is 0
If A = 1, then A’ = 0
If A = 0, then A’ = 1
The truth table for this operation is given below.
| A | Z=A’ |
| 0 | 1 |
| 1 | 0 |
Note: (A’)’ = A
2. Rules associated with AND operation
Consider the 2 variable AND operation.
Z = A.B
The truth table for 2 variable AND operation is given below.
| A | B | Z=A.B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Here we see that Z is 1 when both the variables are 1.
Now some of the rules that we can derive from this are
(i) A.A = A
(ii) A.0 = 0
(iii) A.1 = A
(iv) A.A’= 0
3. Rules associated with OR
Consider the 2 variable OR operation.
Z = A+B
The truth table for 2 variable OR operation is given below.
| A | B | Z= A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Here we see that Z is 1 when any one variable is 1.
Now some of the rules that we can derive from this are
(i) A+A = A
(ii) A+0 = A
(iii) A+1 = 1
(iv) A+A’= 1
4. Distributive Law
- A.(B+C) = A.B + A.C
- A+(B.C) = (A+B).(A+C)
Example: Y=A +A’B. Simplify.
⇒ (A+A’).(A+B) [using distributive law]
⇒ (A.A+A.B+A’A+A’B)
⇒ A+B [using AND law 1 = A, Here consider A+B as A]
Note: The following result is also used as a property in solving problems.
A+A’B= A+B
5. Commutative Law
- A+B= B+A
- A.B = B.A
This is simple law which states that the order in which the AND/OR is applied in expression doesn’t matter.
6. Associative Law
- A.(B.C) = A.(B.C)
- A+(B+C)=(A+B)+C
This law allows the removal of brackets from an expression and regrouping of the variables.
7. De Morgan’s Law
- (A+B)’=A’.B’
- (A.B)’=A’+B’
De morgan’s law consists of two theorems but at this stage knowing the rule is enough.
With this, we have covered all the important rules which are required to solve the problems using Boolean algebra.
Another question then how to start a problem? It’s simple just always remember the priority pyramid while solving the Boolean algebra.
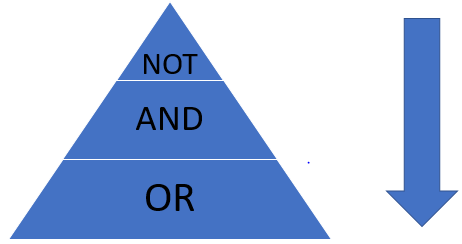
Just follow the arrow’s direction in the pyramid to give priority to the type of operation while solving a problem.
Let’s tabularize all the rules which we have learnt till now
| Compliment | (A’)’=A |
| AND | A.A=A
A.0=0 A.1=A A.A’=0 |
| OR | A+A=A
A+0=A A+1=1 A+A’=1 |
| Associative | A+BC=(A+B).(A+C)
A.(B+C)=A.B+A.C |
| Distributive | A+A’B=A+B
A’+AB=A’+B |
| De Morgan’s Law | (A+B)’=A’+B’
(A.B)’=A’+B’ |
Now let’s take up some examples to help you all understand better
EXAMPLE 1
Y= AB+AB’
- Y=A.B + A.B’ {Taking A common from expression}
- Y=A.[B+B’] {Now using OR law}
- Y=A.1 { Now using AND law}
- Y= A
EXAMPLE 2
Y= AB+AB’C+AB’C’
- Y= AB+AB’C+AB’C’ {Taking A common from expression}
- Y= A [B+B’C+B’C’]
- Y=A[B+B'(C+C’)] {Taking B’ common from expression}
- Y=A[B+B'(1)] {Now using OR law }
- Y=A[B+B’] {Now using OR law}
- Y=A[1]
- Y=A
EXAMPLE 3
Y=(A+B+C)(A+B’+C)(A+B+C’)
- Y=(A+B+C)(A+B’+C)(A+B+C’)
- Let X=A+B
- Y=(X+C)(A+B’+C)(X+C’)
- Y=(X+C)(X+C’)(A+B’+C)
- Y=(X+C.C’)(A+B’+C)
- Y=(X+0)(A+B’+C)
- Y=X.(A+B’+C)
- Y=(A+B).(A+B’+C)
- Y=A+B.(B’+C)
- Y=A+B.B’+B.C
- Y=A+0+B.C
- Y=A+BC
Author:
Adarsh Chauhan
Vidyalankar Institute of Technology
Mumbai
