In this article, we will learn another numbering system, known as octal number system. It has a base of eight (8). It means that there are eight digits with the help of which we can represent any number of the octal family. The digits are from 0 to 7 i.e. (0, 1, 2, 3, 4, 5, 6, 7).
Representation of octal number
It is represented as (X)8
where, X is the octal number and the base 8 is written as suffix or radix.
example: (11)8, (7354)8, (265)8, (56)8, etc. are the examples of an octal number.
Consider an octal number (10101110)8 as shown below. Here leftmost digit is known as a most significant digit (MSD) and rightmost digit is known as a least significant digit (LSD).

Octal to Decimal conversion
Expand the number given in octal form in the power of 8 and sum the values, the result which we will get will be in the decimal form. For example-
(372)8 = 82 × 3 + 81 × 7 + 80 × 2
= 64 × 3 + 8 × 7 + 1 × 2
= 192 + 56 + 2
= 250
= (250)10
Take another example.
(3127)8 = 83 × 3 + 82 × 1 + 81 × 2 + 80 × 7
= 512 × 3 + 64 × 1 + 8 × 2 + 1 × 7
= 1536 + 64 + 16 + 7
= 1623
= (1623)10
Decimal to Octal conversion
Divide the number by 8 and take only the remainder, if the division is completed than take only the remainder which gives the octal number. First of all, MSD is written on the left and move until LSD is reached.
Consider an example.
Find the octal equivalent for decimal 610.
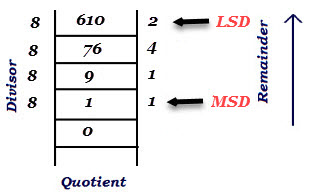
MSD = most significant digit = 1
LSD = least significant digit = 2
We have to write remainder values moving from bottom to top (left to write on paper) as shown above.
Therefore, the octal equivalent for decimal 610 is (1142)8.
Here is the table for octal equivalent of first 16 decimal numbers.
| Decimal number (base = 10) | Octal number (base = 8) |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 14 | 16 |
| 15 | 17 |
