Gray code is a binary numeral system where two successive value differs only in 1 bit. This code is given by Frank Gray. This is the reason why it is called as Gray code. It is an unweighted code. Gray code is also known as reflected binary code or unit distance code or minimum error code or cyclic code.
A binary number is converted to gray code to reduce the switching operation. Consider the gray codes for the 4-bit binary numbers in the following table.
As told earlier that the reflected binary code is the code where two successive value differs only in 1 bit. For example, decimal numbers 3 and 4 are represented by gray code numbers 0 0 1 0 and 0 1 1 0, these numbers differ only in the single bit i.e. bit g2. On the other hand, decimal numbers 3 and 4 are represented by binary code numbers 0 0 1 1 and 0 1 0 0, these numbers differ in 3 bits i.e. bits g0, g1and g2. This is how reflected binary code reduces the switching operation as compared with binary code.
Let us take another example. decimal numbers 7 and 8 are represented by gray code numbers 0 1 0 0 and 1 1 0 0, these numbers differ only in the single bit i.e. bit g3.
| Decimal | Binary
b3 b2 b1 b0 |
Gray code
g3 g2 g1 g0 |
| 0 | 0 0 0 0 | 0 0 0 0 |
| 1 | 0 0 0 1 | 0 0 0 1 |
| 2 | 0 0 1 0 | 0 0 1 1 |
| 3 | 0 0 1 1 | 0 0 1 0 |
| 4 | 0 1 0 0 | 0 1 1 0 |
| 5 | 0 1 0 1 | 0 1 1 1 |
| 6 | 0 1 1 0 | 0 1 0 1 |
| 7 | 0 1 1 1 | 0 1 0 0 |
| 8 | 1 0 0 0 | 1 1 0 0 |
| 9 | 1 0 0 1 | 1 1 0 1 |
| 10 | 1 0 1 0 | 1 1 1 1 |
| 11 | 1 0 1 1 | 1 1 1 0 |
| 12 | 1 1 0 0 | 1 0 1 0 |
| 13 | 1 1 0 1 | 1 0 1 1 |
| 14 | 1 1 1 0 | 1 0 0 1 |
| 15 | 1 1 1 1 | 1 0 0 0 |
Binary to gray code Conversion
The steps for the binary to gray code conversion are
Step-1: MSB (most significant bit) of gray code is same as MSB of binary number.
Step-2: To get next bit of gray code, add MSB with the next bit of binary number (move from left to right). Write the sum and neglect the carry.
Step-3: Repeat the step-2 until reach last bit of the binary number.
Consider an example. Convert binary number (1011) to gray code.
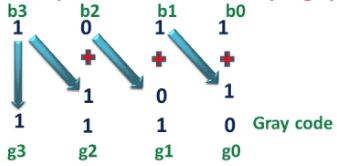
b3, b2, b1, b0 are the bits of the binary number. g3, g2, g1, g0 are the bits of gray code.
Step-1: g3 = b3 = 1
Step-2: g2 = b3 + b2 = 1 + 0 = 1
Step-3: g1 = b2 + b1 = 0 + 1 = 1
g0 = b1 + b0 = 1 + 1 = 0 (neglect carry i.e. 1)
Therefore, the gray code for the binary number 1011 is 1110
Gray Code Applications
1. It is used in error correction.
2. It is used in boolean circuit minimization.
3. It is used in position encoders.
Gray Code Advantages
1. It can be used to minimize a logic circuit.
2. It minimises error while converting analog to digital signals.
Gray Code Disadvantages
1. It is not suitable for arithmetic operations.
2. It is limited to a few practical applications.
