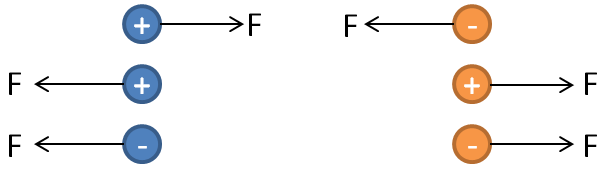
Coulomb’s law allows us to calculate the electrostatic force acting between two electric charges. Force can be repulsive or attractive depending upon the type of electric charge. There is a force of repulsion if both are like charges. There is a force of attraction if both are unlike charges. We can experimentally verify this law.
Coulomb’s Law definition
This law states that the magnitude of the force acting between two point charges at rest is directly proportional to the product of the magnitude of two charges and inversely proportional to the square of the distance between them.
It is noted that point charges are those charges that have negligible size as compared to the distance from the point of observation. The distance between the two charges is the shortest distance. The force acts along the line joining two charges. This force is dependent on the medium in which charges are present.
Coulomb’s Law formula
Consider two charges Qa and Qb as shown in the following figure.
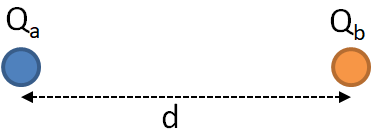
According to Coulomb’s law, the force between charges if given by
$\\(i)\; F\propto Q_{a}Q_{b}\\ \\ (ii)\; F\propto \frac{1}{d^{2}}\\ \\ \therefore F\propto \frac{Q_{a}Q_{b}}{d^{2}}$
Removing proportionality, we get
$F= k\frac{Q_{a}Q_{b}}{d^{2}}$
where, F is the force acting between charges Qa and Qb.
d is the shortest distance between charges Qa and Qb.
k is Coulomb’s constant or electrostatic force constant.
The formula of k is given by
$k = \frac{1}{4\pi \varepsilon }=\frac{1}{4\pi \varepsilon _{o}\varepsilon _{r} }$
where, ε is the permittivity
εr is the relative permittivity. It is also known as dielectric constant of the medium.
εo is the absolute permittivity of free space. Its value is 8.854 × 10-12 C2 N-1 m-2
The formula of Coulomb’s constant can be simplified as
$\\k =\frac{1}{4\pi \times 8.854\times 10^{-12} \times \; \varepsilon _{r} }\\\\ k=\frac{9\times 10^{9}}{\varepsilon _{r}}$
Now, the Coulomb’s force can be written as
$F=\frac{1}{4\pi \varepsilon _{o}\varepsilon _{r}}\frac{Q_{a}Q_{b}}{d^{2}}$
OR
$F=\frac{9\times 10^{9}}{\varepsilon _{r}}\frac{Q_{a}Q_{b}}{d^{2}}$
It is noted that coloumb’s force is valid for small as well as large distances. This force between two electric charges is not affected by the presence of other electric charges. In other words, we can say that coulomb’s force is a two body interaction.
Consider the following figure. There are two charges. We can conclude that like charges experience repulsive force whereas unlike charges experience an attractive force.