Transfer function Definition
A transfer function is expressed as the ratio of Laplace transform of output to the Laplace transform of input assuming all initial condition to be zero.
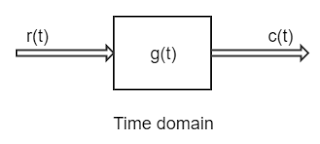
Consider a system whose time domain block diagram is
Contents
show
where, r(t) = input and c(t) = output
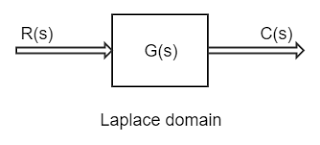
Now taking Laplace transform then
Now the transfer function G(s) is given by
Note: Transfer function for any input is same for a given circuit.
While taking the Laplace transform for determining the transfer function of a control system, it is assumed that all initial condition concerning the differential equations are zero. The transfer function of a given system is a fixed quantity. The output of the system can be evaluated simply by taking the inverse Laplace of the product of transfer function and the given input.
Therefore, output is given by
C(s) = G(s) x R(s)
then, output in the time domain can be evaluated by taking inverse Laplace as
Advantages of Transfer function
1. If transfer function of a system is known, the response of the system to any input can be determined very easily.
2. A transfer function is a mathematical model and it gives the gain of the system.
3. Since it involves the Laplace transform, the terms are simple algebraic expressions and no differential terms are present.
4. Poles and zeroes of a system can be determined from the knowledge of the transfer function of the system.
Disadvantages of Transfer function
1. Transfer function does not take into account the initial conditions.
2. The transfer function can be defined for linear systems only.
3. No inferences can be drawn about the physical structure of the system.