There are some simple relations between currents and voltages of different branches of an electrical circuit. These relations are determined by some elementary laws that are known as Kirchhoff laws or more exactly Kirchhoff Current and Voltage laws. These laws are first derived by Gustave Robert Kirchhoff and therefore these laws are also called as Kirchhoff Laws.
1. Kirchhoff Current Law
In any electrical network (circuit), the algebraic sum of the currents meeting at a point (or junction) is zero.
OR
In other words, the total current leaving a junction is equal to the total current entering that junction.
Note: Kirchhoff Current Law is also called as Kirchhoff Point Law.
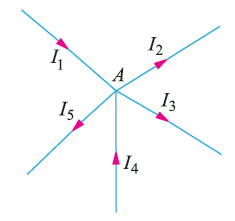
Consider the figure1 as shown. Point A is the junction. Currents I1, I4 leading to point A and currents I2, I3, & I5 leading away from the junction A. Let the incoming currents to be positive and the outgoing currents to be negative. According to Kirchhoff Current Law, we have
Σ I = 0
I1+(−I2)+(−I3)+I4+(−I5)=0
or
I1+I4= I2+I3+I5
i.e. sum of incoming currents = sum of outgoing currents
therefore, According to Kirchhoff Current Law
Σ I = 0
2. Kirchhoff Voltage Law
The algebraic sum of the products of currents and resistances in each of the conductors in any closed path (or mesh) in a network plus the algebraic sum of the e.m.fs. in that path is zero.
Σ IR + Σ e.m.f. = 0
While applying Kirchhoff Voltage Law, polarities of the voltage drop should be taken account.
How to apply Kirchhoff Voltage Law
Choose a junction and go round the mesh till we come back to the starting point. During this path take an algebraic sum of voltage drop and e.m.f. and set it to zero.
Note: Kirchhoff Voltage Law is also called as Kirchhoff Mesh Law.
Note: Every voltage being given its proper sign, plus or minus.
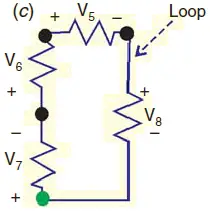
Consider figure2. According to Kirchhoff Voltage Law, we have
Let starting node is shown in green colour. Going in clock wise direction in the loop, we have
−V7−V6−V5−V8=0
